On dit souvent qu'un ordinateur ne fonctionne qu'avec des 0 et des 1. Bien que vraie, cette assertion peut sembler vague, car elle n'explicite ni comment l'ordinateur fonctionne physiquement, ni comment un programme peut s'exécuter dans cet environnement. Ceci est pourtant le fondement de l'informatique, et mérite ainsi que l'on s'y appesantisse.
Étymologiquement, « informatique » est un mot dérivé d'information. On définit couramment ce terme par « traitement automatique de l'information ».
De la Nature de l'information
Commençons par un aparté sur l'information. Le terme français regroupe beaucoup de sens. Certains sont assez précis (par exemple, un journal télévisé). Ici nous considérons un sens plus large, et surtout, plus mathématique. En effet, il est possible de définir formellement l'information, et même d'en mesurer la quantité !
L'Information comme mesure d'incertitude
Des mathématiciens se sont penchés sur le sujet et ont défini l'information comme une mesure d'incertitude. Détaillons.
Je mets le GPS pour me rendre à un rendez-vous, et je roule actuellement sur une départementale rectiligne. Le GPS me dit « Continuez tout droit ». Ce message est dénué d'intérêt, je n'ai pas d'autre choix que d'aller tout droit. L'incertitude sur la teneur du message était très faible (presque 0%), il n'y avait aucune chance pour que le GPS me dise soudainement de couper à travers champs en sortant de la route ! Un peu plus loin, j'arrive à un carrefour en croix. Je peux aller à droite, à gauche, ou tout droit. Le GPS me dit alors « Continuez tout droit ». Cette fois-ci, bien que les mots soient les mêmes, le message est bien plus teneur d'information. Parmi les trois choix qui s'offrent à moi, ce message m'en désigne un en particulier. L'incertitude était d'environ 67% (deux tiers), donc beaucoup plus élevée qu'au moment de la départementale rectiligne.
L'Information comme principe structurant
Cet exemple illustre la notion d'incertitude. Mais par exemple, on peut dire qu'une photo, qu'un disque, qu'une bobine de film ou qu'un texte contiennent de l'information. Comment parler d'incertitude dans ces cas ? Une réponse est apportée par l'ingénieur Claude Shannon en 1948 dans sa Théorie Mathématique de la Communication. L'information est ce qui va distinguer du hasard.
Prenons le cas d'une image, pour simplifier en noir et blanc (ou plutôt, en nuances de gris). On peut la considérer comme un ensemble de points (des pixels par exemple), chaque point ayant une luminosité entre 0 (noir) et 100 (blanc). Une image quelconque, tirée au hasard, est une image dont la luminosité de chaque point est tirée au sort. Dans la Figure 1, l'image (a) est produite ainsi, chaque pixel prend une nuance de gris aléatoire entre blanc et noir. On la compare à l'image (b), tirée d'une véritable photographie.

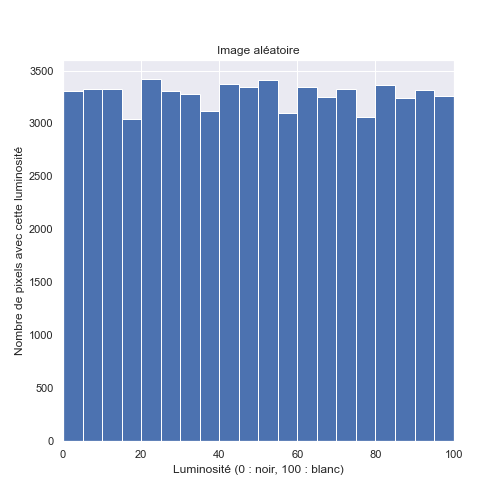

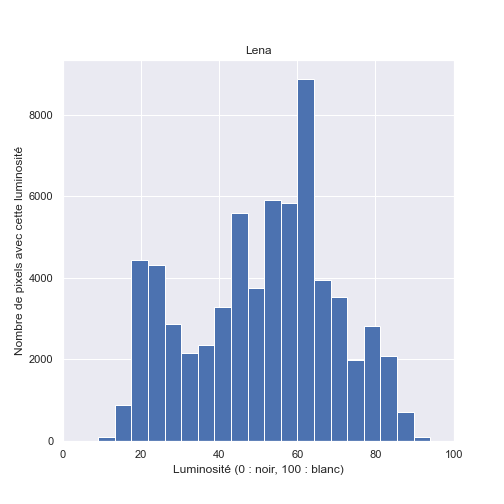
En dessous des images, nous avons affiché la distribution des luminosités, c'est-à-dire que l'on compte, pour chaque niveau de luminosité (plus exactement pour chaque tranche de niveaux), combien de pixels possèdent cette (ces) valeur(s). Pour l'image (a), on voit qu'il y a à peu près autant de pixels de chaque niveau de luminosité. C'est normal, car en tirant au hasard sans tricher, on a la même chance (la même probabilité) de choisir chaque niveau de luminosité. Mais dans le cas de l'image (b), le graphe est beaucoup plus irrégulier. On observe notamment un pic entre 60 et 64. Ces pixels ne sont pas tirés au hasard, ils suivent une certaine logique. L'information, c'est cette différence entre la distribution aléatoire et la distribution réelle.
L'exemple porte sur les images, mais peut s'appliquer à tout support. Un bruit blanc ne contient pas d'information, le signal est aléatoire ; mais lors de l'enregistrement d'un concert, le signal enregistré suit une certaine logique et contient de l'information. De même pour un texte, pour une vidéo, etc. On retrouve en fait le principe évoqué dans cet article du blog consacré à l'intelligence artificielle, au paragraphe « Information et statistique ». Ces représentations de l'information ne sont pas laissées au hasard, mais représentent une réalité, qu'une analyse statistique peut permettre de révéler.
Cette définition de l'information est une extension de celle écrite un peu plus haut, comme mesure de l'incertitude. Reprenons le cas de l'image, dans la Figure 1. Conceptuellement c'est comme si nous générions une image en nuance de gris. Presque à chaque fois, nous obtiendrions une image similaire à l'image (a), tirée aléatoirement, car ces images aléatoires constituent la quasi totalité des images en nuances de gris possibles. Mais si par miracle, nous obtenions l'image (b), nous serions surpris. Obtenir une telle image était très incertain, l'image (b) est donc porteuse de plus d'information que l'image (a).
Représenter l'information
Maintenant que la notion d'information s'est précisée, revenons à ce qui nous intéresse : le traitement de cette information par un ordinateur. Concrètement, un ordinateur est un appareil électronique, composé de circuits imprimés et de câbles électriques. Avant de pouvoir traiter une information, il va nous falloir un moyen pour la manipuler. Ce n'est bien sûr pas avec trois câbles et quatre interrupteurs que l'on va pouvoir maîtriser un concept si abstrait, n'est-ce pas ? Eh bien, peut-être que si, grâce à une technique développée il y a quelques centaines de milliers d'années par Homo sapiens : le langage. Car d'une idée abstraite l'information va devenir quelque chose de tangible, de physique, plus facile à appréhender.
Un exemple de manipulation intuitive de l'information : la communication orale
La capacité à transmettre de l'information fut une des premières révolutions dans les méthodes utilisées par l'Homme pour manipuler l'information, et fut certainement déterminante lors de son évolution. Si une tribu ne communique que par cris et gestes alors qu'une autre possède un langage, cette dernière possède un avantage certain. L'information est plus rapide à transmettre, plus facilement compréhensible, beaucoup plus précise.
Concrètement, Homo sapiens est parvenu à « encoder » de l'information en utilisant des séquences de sons. L'information est transmise par un changement de forme, de support. Initialement, il s'agit d'une idée qui germe dans la tête de l'émetteur. Quelques synapses qui s'activent dans le cerveau. En parlant, l'émetteur traduit cette idée en onde sonore, des vibrations dans l'air, qui arrive à l'oreille du destinataire. Ce dernier traduit dans le sens inverse cette onde sonore en activations de synapses. Durant cet échange, l'information change de support, mais pas de nature.
Cette traduction mutuelle implique que les deux individus se soient mis d'accord sur une « langue » commune, c'est-à-dire une façon standardisée de représenter tel ou tel bout d'information. Il s'agit d'une convention, d'une fabrication humaine. Et si elle est assez précise, le destinataire aura en tête la même information que l'émetteur.
Plusieurs supports, une seule idée
Plus tard, avec la naissance de l'écriture, une nouvelle forme intermédiaire de transmission de l'information apparaît : des symboles, dessinés, peints ou gravés. Le support est différent mais le principe reste identique. Une suite de hiéroglyphes encode l'information que désire inscrire l'émetteur, et toute personne sachant lire les hiéroglyphes peut décoder cette information.
Un autre support existe : il s'agit des nombres. On peut représenter beaucoup d'information avec des nombres. Dans le cas d'un texte, on peut utiliser la convention suivante :
- A = 1,
- B = 2,
- C = 3,
- ...
En supposant que l'on étende suffisamment le nombre de caractères encodés, n'importe quelle phrase peut s'exprimer sous la forme d'une séquence de nombres. Essayer par exemple de décoder la phrase suivante :
2 15 14 10 15 21 18 20 15 21 20 12 5 13 15 14 4 5
Pour une couleur, on peut utiliser trois nombres sous la forme RVB (Rouge Vert Bleu). N'importe quel signal physique (grandeur mesurée au cours du temps) peut être représenté par la valeur mesurée à des intervalles de temps définis, c'est ce qu'on appelle l'échantillonnage. Et ainsi de suite. Toute information ne pourrait donc qu'être nombres. Bien sûr, la représentation n'est pas parfaite. Par exemple, la notation RVB classique ne permet d'exprimer que 16 millions de couleurs, alors qu'il en existe une infinité. Mais 16 millions, c'est déjà assez pour les communications humaines. Les concessions sont légères.
Au Cœur de l'informatique
Et si nous devions trouver un nom pour ce format, fait à partir de nombres, ce serait... numérique.
En effet, on arrive très exactement à la représentation de l'information qu'utilisent les ordinateurs. À la différence près que les nombres qu'ils manipulent ne sont pas exprimés en décimal (base 10) mais en binaire (base 2). Au lieu d'utiliser dix symboles (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) pour écrire les nombres, ils n'en utilisent que deux (0 et 1). Physiquement, un interrupteur allumé représente un 1, et un interrupteur éteint représente un 0. On appelle cela un bit d'information (en anglais, bit signifie un bout, un morceau). Prenez des milliers, des millions, des milliards d'interrupteurs, et vous pourrez représenter (presque) toute l'information que vous souhaiterez avec un ordinateur.
Pour des raisons pratiques, on utilise souvent la notion d'octet, soit huit bits d'affilé, pour parler de quantité d'information. Et ses déclinaisons, le kilooctet (Ko), le mégaoctet (Mo), le gigaoctet (Go), le téraoctet (To), etc.
Comme le système binaire va renevir au cours de cet article, voici, à droite, un petit tableau de conversion :
Comme pour les nombres décimaux, le chiffre le plus à droite est celui des unités. En se déplaçant vers la gauche, on monte d'un cran dans la numération. Pour le système décimal, on monte d'une puissance de dix (dizaine, centaine, milliers, etc.), pour le système binaire, on monte d'une puissance de deux (deux-aine, quatre-aine, huit-aine, seize-aine, etc.).
Comme pour les nombres décimaux, rajouter un 0 devant un nombre binaire ne change pas sa valeur. Donc 3 peut s'écrire en binaire 11, 011 ou même 0011.
| Nombre décimal | Nombre binaire |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
Si l'on souhaite enregistrer le message « Bonjour » sur un ordinateur, nous allons donc :
- Encoder cette information numériquement, en utilisant par exemple la convention citée plus haut (A=1, B=2, etc.)
- Traduire l'encodage décimal en encodage binaire.
- Positionner des interrupteurs dans les états ouverts/fermés correspondant.
En guise d'interrupteur, on utilise un composant nommé transistor. Il s'agit d'une version miniature du même principe. Si on considère un câble électrique comme une route, le transistor est un péage que l'on contrôle électriquement. Allumé, le transistor laisse passer le courant. Éteint, il devient bloquant. Dans un processeur, la centrale à calculs de l'ordinateur, on peut trouver plusieurs milliards de ces transistors, car ces derniers ne mesurent désormais qu'une dizaine de nanomètres (seulement 100 fois la taille d'un atome). Ils permettent à l'ordinateur de représenter toute l'information que l'on souhaite.
Manipuler l'information : le calcul
Regardons d'où l'on vient. L'information est un concept, abstrait, qui mesure l'incertitude, qui se repère par les propriétés structurantes de son support d'expression. Ces supports peuvent être très divers, de l'écriture au son, en passant par des listes de nombres. Un ordinateur utilise ces nombres, écrits sous forme binaire, pour se représenter l'information. De son point de vue, il dispose donc d'un ensemble d'interrupteurs, ouverts ou fermés. Il va donc falloir se contenter de ça pour pouvoir traiter cette information.
Avant de commencer, une petite remarque. Si l'ordinateur en question est un agent de conversation, on lui donne des phrases, encodées en nombres, et on attend de lui qu'il réponde par d'autres phrases, donc qu'il produise d'autres nombres. Conceptuellement, l'ordinateur ne fait que prendre des nombres et en déduire, par le calcul, des nouveaux. La seule tâche réalisée par un ordinateur est donc du calcul, bête et méchant.
De la Logique électronique à l'arithmétique
Les transistors peuvent être agencés de manière à implémenter une logique, c'est-à-dire quelques opérations très basiques :
- le NON : Si on a un 1 en entrée, on renvoie 0. Si on a un 0 entrée, on revoie un 1.
- le ET : Sur deux entrées, si les deux sont à 1, on renvoie 1. Si au moins une vaut 0, on renvoie 0.
- le OU : Sur deux entrées, si au moins l'une vaut 1, on renvoie 1. Si les deux entrées sont à 0, on renvoie 0.
- le OU exclusif : Sur deux entrées, si les deux sont égales (00 ou 11), on renvoie 0. Sinon (01 ou 10), on renvoie 1.
À partir de cela, on peut construire, en enchaînant les blocs précédents, le NON-OU (un OU suivi d'un NON) et le NON-ET (un ET suivi d'un NON). Ces opérations sont réalisées au niveau électronique. Grossièrement, un 1 signifie que le courant passe dans le fil, un 0 signifie que le courant ne passe pas. Si l'on envoie du courant dans les deux entrées d'un ET, il y aura du courant en sortie.
Les petits modules qui réalisent ces opérations logiques sont appelées des portes logiques. Voici un site qui présente les circuits électroniques qui se cachent derrière. Si vous avez déjà joué à Minecraft, ce sont les mêmes portes logiques que l'on peut réaliser avec de la redstone !
On utilise ensuite ces portes logiques comme des petits blocs que l'on assemble pour créer un système plus complexe.
L'Additionneur
Voici par exemple comment construire un additionneur. Comme son nom l'indique, ce module va faire des additions. Dans un premier temps, nous allons uniquement considérer l'addition de deux bits. Voici ce qu'on aimerait bien avoir :
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10
Si ce n'est pas très clair, reportez-vous au tableau de conversion décimal-binaire un peu plus haut. Pour uniformiser, rajoutons des zéros aux résultats, qu'ils aient tous la même taille :
- 0 + 0 = 00
- 0 + 1 = 01
- 1 + 0 = 01
- 1 + 1 = 10
Maintenant, nous sommes à la recherche d'une « formule logique » pour lier les entrées aux sorties.
Commençons par le chiffre des unités (celui tout à droite). Quand les deux entrées sont égales (soit deux 0, soit deux 1), ce nombre est à 0. Dans les autres cas, ce nombre est à 1. C'est la définition du OU exclusif, nous pouvons donc calculer ce chiffre à l'aide d'une porte logique !
Ensuite, pour le chiffre des « dizaines », ou plutôt « deuzaines » dans ce contexte binaire (celui tout à gauche). Il vaut tout le temps zéro, sauf lorsque les deux entrées sont à 1. C'est la définition du ET, nous pouvons donc également le calculer avec une porte logique.
Voilà, il ne nous en faut pas plus. La vidéo ci-dessous montre le résultat de notre assemblage, grâce au site logic.ly. Les deux interrupteurs représentent les deux bits à additionner. La porte OU exclusif contrôle le chiffre de droite. La porte ET contrôle le chiffre de gauche.
Nous avons réussi à additionner deux bits. Dans un cas plus général, nous aimerions pouvoir additionner des nombres plus grands, et donc plusieurs bits ensembles. Pour ce faire, nous allons utiliser la même méthode qu'enseignée à l'école pour apprendre les additions : poser les calculs.
On additionne les chiffres en colonnes de droite à gauche, et si on dépasse 10 (ou 2 en décimal), on compte une retenue que l'on propage à la colonne suivante. Pour chaque colonne, on ne fait qu'une addition de deux bits, plus éventuellement une retenue. Ainsi, pour construire notre additionneur complet, on commence par modifier un peu celui de deux bits, pour prendre en compte la retenue :
Les deux bits par colonne à additionner sont les deux interrupteurs du haut. L'interrupteur en bas est utilisé pour prendre en compte l'éventuelle retenue de la colonne précédente. En sortie, nous avons deux chiffres. Le chiffre en sortie pour la colonne, et le chiffre de la retenue.
Maintenant, il suffit de mettre bout-à-bout ces additionneurs en reliant les retenues entre elles et en notant les sorties pour chaque colonne. Voici ce que ça donnerait (avec à droite les nombres en décimal) :
Voilà, nous avons une machine totalement électronique qui réalise des additions. Bien sûr, on peut complexifier, supporter plus de nombres, de plus grands nombres, faire des soustractions, des multiplications, etc. Le fonctionnement, bien que plus complexe, sera analogue. Voici donc comment un ordinateur manipule ces 0 et ces 1.
Conclusion
Les ordinateurs fonctionnent en traitant de l'information. Le fond de l'information est sa force structurante qui la différencie d'un résultat du hasard. Ce fond peut revêtir plusieurs formes. La forme adoptée pour les ordinateurs est le numérique, où tout est encodé sous forme de nombres. À l'intérieur de la machine, ces nombres sont écrits et manipulés en binaire par des transistors. Et grâce à des modules électroniques élémentaires nommés portes logiques, il est possible d'effectuer des opérations sur ces nombres, donc de transformer l'information, en calculant d'autres informations à partir de celles qu'on nous a données. Voilà pourquoi on dit qu'un ordinateur, ça ne fonctionne qu'avec des 0 et des 1.
Quelques références pour aller plus loin
À emprunter à la médiathèque :
- 📕 La Théorie de l'information / Aurélien Bellanger.- Paris : Gallimard , 2012.- 486 p. ; 21 cm.- (Blanche ).
Pour revenir sur la notion d'information développée par Shannon :
Une description informationnelle de l'univers :
Une présentation détaillée des principes de la théorie derrière l'information :
Article précédent Article suivant
