Résultats et analyse de l'expérience de sagesse des foules menée à l'occasion de la Fête de la science 2025.

À l'occasion de la Fête de la science 2025, dont la thématique était les « Intelligence(s) », nous avons mis en place une petite expérience de sagesse des foules. Du vendredi 3 au samedi 11 octobre, à l'entrée de la médiathèque, se trouvait un pot rempli de billes avec un panneau invitant à en estimer le nombre. Une urne, un stylo et des bulletins permettaient de partager son estimation. Individuellement, il semble difficile de trouver la bonne réponse. Mais l'idée de la sagesse des foules est de mettre en commun nos prédictions, ce qui peut avoir pour effet de considérablement améliorer notre précision.

Ce phénomène a été mis en lumière pour la première fois en 1906 par le britannique Francis Galton. Il a demandé aux visiteurs d'un marché de bétail d'estimer le poids d'un bœuf, et a obtenu 787 estimations. La médiane (nous revenons sur la signification de cette opération plus bas) des estimations était de 547 kg, pour un poids réel de 543 kg. Ainsi, nous essayons de reproduire cette expérience, sous une forme plus légère.

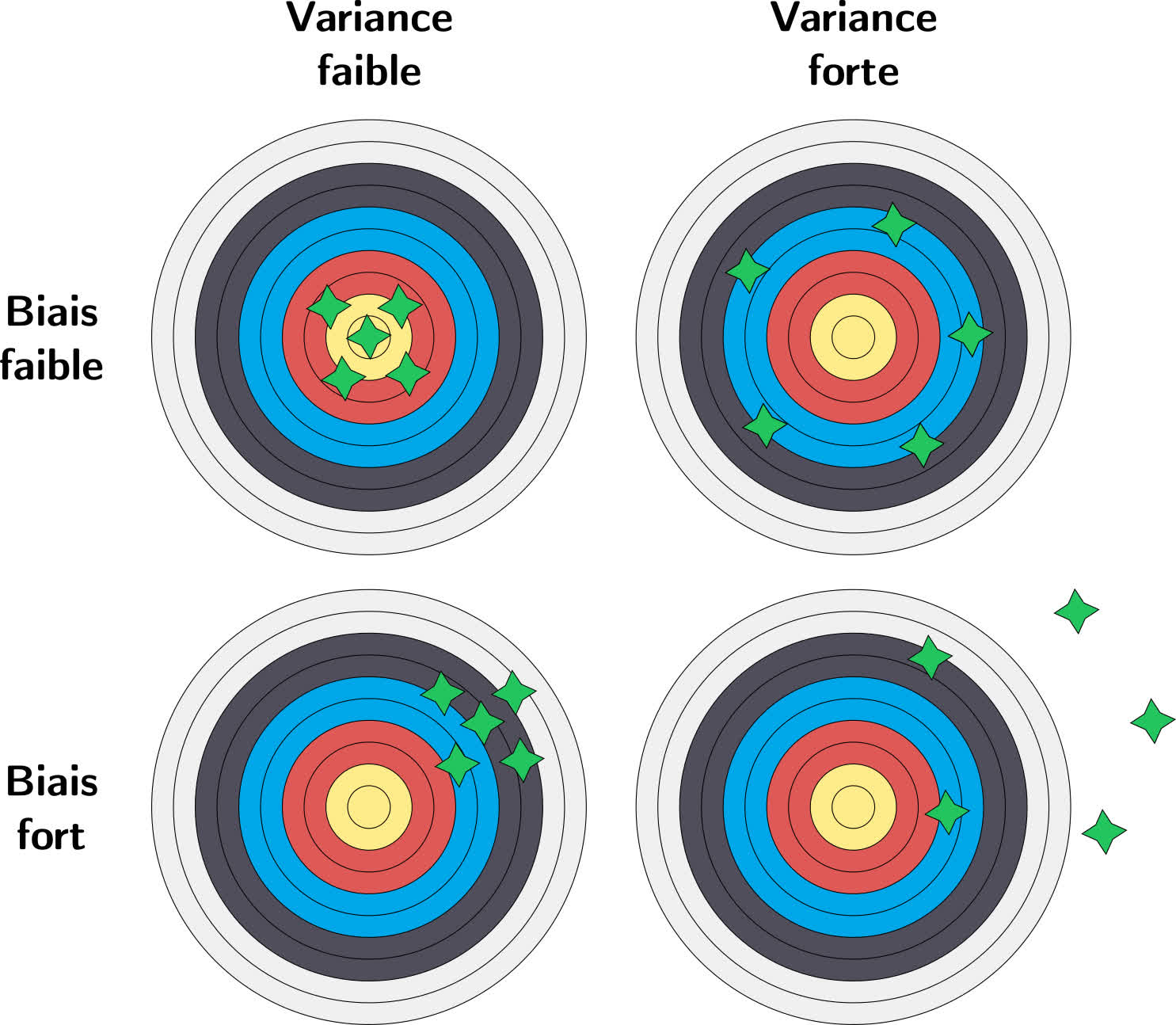
La réussite de l'expérience est conditionnée par l'indépendance des participants au moment de leur jugement. Ils ne doivent être ni biaisés, ni influencés. Idéalement, les estimations sont alors toutes centrées autour de la bonne valeur (pas de biais), et les fluctuations (la variance) se compensent : grossièrement, il y a autant de sous-estimation que de sur-estimation.

Nous avons récolté 370 estimations, allant de 1 à 7299 (nous avons délibérément omis les réponses supérieures à 10000). Le graphique ci-dessous en illustre la distribution, c'est-à-dire, pour chaque valeur possible, le nombre de personnes ayant fait cette estimation. Par exemple, 33 personnes pensaient qu'il y avait entre 200 et 250 billes dans le pot. La barre verticale verte montre la valeur réelle du nombre de billes dans le pot : 708.

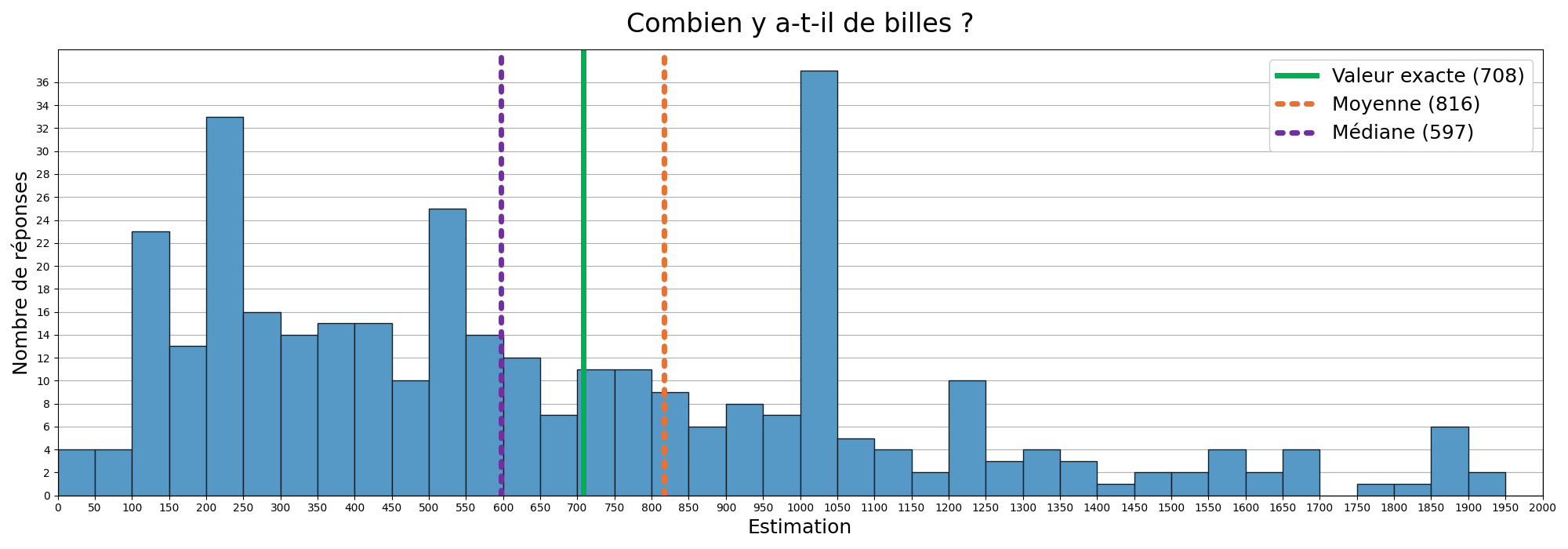
Première remarque, les valeurs sont très dispersées, les gens se sont beaucoup trompés. Une mesure de cela est la précision individuelle. Si une personne répond 500 au lieu de 708, sa précision est de 500 / 708 = 70 %. Pour notre expérience de billes, la moyenne de précision individuelle est de 27,4 %. C'est assez peu précis.

Également, il est possible de mesurer la précision collective, en mettant en commun toutes les estimations. Il y a deux méthodes classiques pour cela : la moyenne et la médiane.

• La moyenne : on ajoute toutes les valeurs et divise la somme par le nombre de valeurs. Dans notre cas, la moyenne est de 816,30 billes, soit une précision collective de 84,7 %.
• La médiane : on sélectionne la valeur telle qu'il y ait autant d'estimations en-dessous qu'au-dessus. Dans notre cas, la médiane est de 597 billes, soit une précision collective de 84,3 %. L'avantage de la médiane par rapport à la moyenne est de réduire l'impact des valeurs extrêmes, mais ici, il semble y avoir un biais assez fort qui tend à sous-évaluer le nombre de billes.

Toutefois, dans les deux cas, la précision collective dépasse la précision individuelle, d'où le concept de sagesse des foules.

Le critère d'indépendance des jugements est crucial pour la réussite de cette expérience. Imaginons qu'un malin réussisse à convaincre 10 personnes ayant estimé 1000 que le pot contient en réalité 500 billes. Ces nouvelles estimations ne seraient pas trop erronées : la précision individuelle augmenteraient à 27,7 %. Cependant, cela briserait l'effet de compensation des erreurs : la précision collective (médiane) chuterait à 77,7 %. Les effets d'influences sont généralement plus subtils, mais rien qu'entendre une personne dire « j'ai mis qu'il y avait 350 billes » suffit à tordre notre jugement.

Pour notre distribution, nous pouvons tout de même identifier un biais évident : les nombres ronds. Au lieu d'une distribution en forme de cloche, on observe plusieurs pics, correspondant à des nombres ronds :

• 1000 a été écrit 27 fois,
• 500, 200 et 100 ont été écrits 12 fois chacun,
• 300 a été écrit 8 fois,
• 1200, 700 et 600 ont été écrits 6 fois,
• puis on passe aux nombres « un peu moins ronds » : 550 et 450 ont été écrits 5 fois,
• …

Pour la réalisation et l'analyse de cette expérience, nous nous sommes beaucoup inspirés du travail de Mehdi Moussaid, chercheur en science cognitive à l'institut Max Planck de Berlin et créateur de la chaîne YouTube Fouloscopie. Suite à ses vidéos, nous avions déjà tenté de reproduire une expérience de propagation des rumeurs. Il a notamment réalisé plusieurs expériences de sagesse des foules pour une vidéo en 2023 (voir ci-dessous). Récemment, il a publié une autre vidéo montrant comment l'influence peut tout même nous aider à trouver collectivement des réponses : Peut-on remporter ‘Qui veut gagner des millions’.. avec 120 JOUEURS ?.

Nous vous invitons à reproduire l'expérience par vous-même, elle demande assez peu de moyens – un pot, une multitude de petits objets (merci à Noé de nous avoir prêté ses billes !), une urne. Pour le dépouillage des bulletins et l'analyse des données, un simple logiciel de tableur peut suffire ; dans notre cas, nous avons utilisé un document texte et un notebook Python.